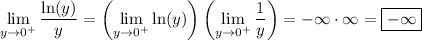It looks like the given limit is
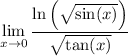
Note that the two-sided limit doesn't exist, since
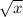 is defined only for for
is defined only for for
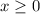 . So I'll further assume you want the one-sided limit as
. So I'll further assume you want the one-sided limit as
 approaches 0 from above.
approaches 0 from above.
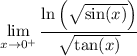
For
 just above zero, we have
just above zero, we have
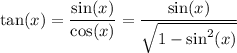
so we can rewrite the limit as
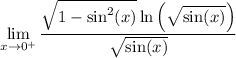
Substitute
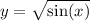 . As
. As
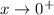 , so does
, so does
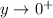 , and
, and
the limit transforms to
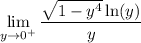
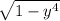 is continuous at
is continuous at
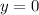 , and
, and
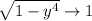 , so we're left with
, so we're left with