Answer: x=55 or x=-55 (this is how it is usually how it is to be be written in the Cambridge syllabus or else you can write 'x=55,-55')
Explanation:
All you have to do is make ' |x|' the subject and then continue as normal simplifications by switching the - 10 to the other side in order to make ' |x|' the subject then when you switch the -10 to the other side it becomes positive 10 (+10)
2|x| -10 = 100
2|x| = 100+10
2|x| = 110
|x| = 110/2 ← (then you should lastly remove the two to make the
|x| = 55 ' |x|' the subject so it becomes division)
therefore x=55 or x=-55
A small note incase you have a confusion :)
and just incase you don't know what |x| means- it is the determinant. And the determinant is the denominator you get while getting the inverse of a matrix (
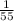 )
)