Question

This is a absolute value equality assignment how do I solve
2|x| -10 = 100 ?

Answer 1

Answer: x=55 or x=-55 (this is how it is usually how it is to be be written in the Cambridge syllabus or else you can write 'x=55,-55')

Explanation:

All you have to do is make ' |x|' the subject and then continue as normal simplifications by switching the - 10 to the other side in order to make ' |x|' the subject then when you switch the -10 to the other side it becomes positive 10 (+10)

2|x| -10 = 100

2|x| = 100+10

2|x| = 110

|x| = 110/2 ← (then you should lastly remove the two to make the

|x| = 55 ' |x|' the subject so it becomes division)

therefore x=55 or x=-55

A small note incase you have a confusion :)

and just incase you don't know what |x| means- it is the determinant. And the determinant is the denominator you get while getting the inverse of a matrix (
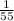`(1)/(55)`)

Answer 2

x = 55, x = -55

Explanation:

→ 2|x| -10 = 100

→ 2lxl = 100 + 10

→ lxl = 110/2

→ [ lxl = 55 ]

Now the absolute value of x will be,

→ lxl = 55

→ x = 55 (or) x = -55

Hence, the value of x is 55,-55.