Answer:

Explanation:
The inverse of a function
 is denoted by f
is denoted by f
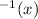
To find the inverse of

Set
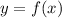
So

Express x in terms of y

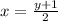
So inverse is


Replace y with x to make it a function of x


To test if this correct, note that the property of an inverse function is that it undoes the original function. In other words if we have f(a) = k then f⁻¹(k) = a
Let's test this with some reasonable value for x
f(2) = 2.2 - 1 = 3
f⁻¹(3) = (3+1)/2 = 2
Hence correct