Answer:
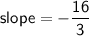
Explanation:
Let's understand this notation:
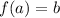 means that at x = a, there exists value y = b. We can write
means that at x = a, there exists value y = b. We can write
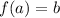 in the coordinate form of
in the coordinate form of
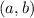 .
.
So according to the problem, we can rewrite the notation in form of coordinate as:
 and
and

Finding slope, we can use the slope formula of:

Since y = f(x) then:
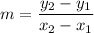
Determine that:
Substitute in the formula:
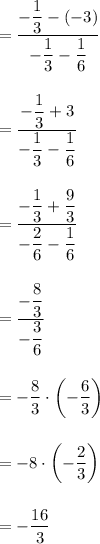
Therefore, the slope is -16/3