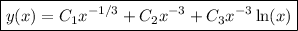Substitute
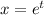 . By the chain rule,
. By the chain rule,
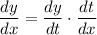
Now
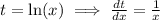 , so
, so
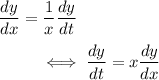
Differentiate both sides again to recover the second and third derivatives.
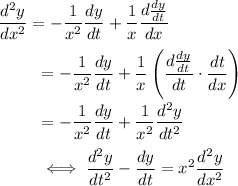
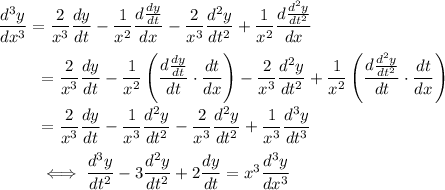
The ODE then transforms to a linear one,
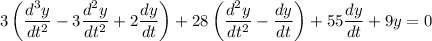
or using Lagrange's prime notation,
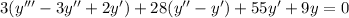
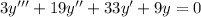
The characteristic equation is
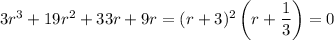
with roots at
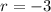 and
and
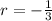 , so the general solution is
, so the general solution is
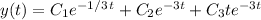
Back in terms of
 , we get
, we get