Question

Please help me, im stuck on this question

Answer 1

Part a.

i. -20.6(m/s).

ii. -19.16(m/s).

iii. -19.016(m/s).

Part b.

-19m/s.

Explanation:

Let's refer to the average velocity formula:

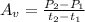`A_v=(P_2-P_1)/(t_2-t_1)`; where
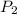`P_2` and
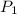`P_1` are the final position, and initial position, respectively. Also,
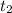`t_2` and
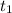`t_1` are the final time, and initial time, respectively.

For part (i).

1. Find
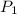`P_1` and
`P_2`.

`P_1=45(2)-16(2)^2=26\\ \\P_2=45(2.1)-16(2.1)^2=23.94`

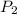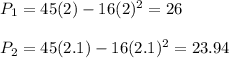
2. Calculate average velocity.

`A_v=(P_2-P_1)/(t_2-t_1)=(23.94m-26m)/(2.1s-2s) =-20.6m/s.`

--------------------------------------------------------------------------------------------------

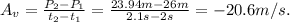
For part (ii).

1. Find
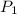`P_1` and
`P_2`.

`P_1=45(2)-16(2)^2=26\\ \\P_2=45(2.01)-16(2.01)^2=25.8084`

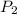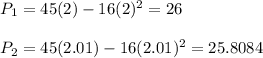
2. Calculate average velocity.

`A_v=(P_2-P_1)/(t_2-t_1)=(25.8084m-26m)/(2.01s-2s) =-19.16m/s.`

--------------------------------------------------------------------------------------------------

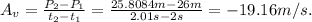
For part (iii).

1. Find
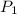`P_1` and
`P_2`.

`P_1=45(2)-16(2)^2=26\\ \\P_2=45(2.001)-16(2.001)^2= 25.980984`

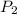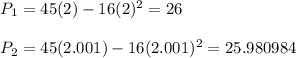
2. Calculate average velocity.

`A_v=(P_2-P_1)/(t_2-t_1)=(25.980984m-26m)/(2.001s-2s) =-19.016m/s.`

--------------------------------------------------------------------------------------------------

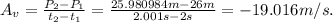
For part b.

Formula of instantaneous velocity:

`V_I=(dx)/(dt) .`

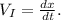
The instantaneous velocity indicates that we need to find the derivative with respect to time (t) of the position equation, and evaluate it for the indicated time. Let's do that:

`y'=(1)45t^(1-1) -(2)16t^(2-1) \\ \\y'=45-32t`

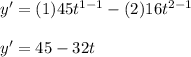
Now, we evaluate for the indicated time (t= 2).

`y'=45-32(2)=-19m/s.`

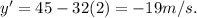
Hence, the instantaneous velocity for t= 2 is -19m/s.

Answer 2

a) i) -20.6 ft/s

ii) -19.16 ft/s

iii) -19.016 ft/s

b) -19 ft/s

Explanation:

Given information:

• Height: s(t) = 45t - 16t²

`\boxed{\begin{minipage}{4 cm}\underline{Average velocity formula}\\\\ $\overline{v}=(s(t_2)-s(t_1))/(t_2-t_1)$\\\end{minipage}}`

where:

• t₁ = initial time
• t₂ = final time
• s(t₁) = position function at t₁
• s(t₂) = position function at t₂

Part (a)

Question (i)

Given interval: [2, 2.1]

`\implies t_1=2`

`\implies t_2=2.1`

`\implies s(t_1)=45(2)-16(2)^2=26`

`\implies s(t_2)=45(2.1)-16(2.1)^2=23.94`

Substitute the values into the formula and solve for v:

`\begin{aligned}\overline{v} & =(s(t_2)-s(t_1))/(t_2-t_1)\\\\\implies \overline{v} & =(s(2.1)-s(2))/(2.1-2)\\\\& =(23.94-26)/(2.1-2)\\\\& =(-2.06)/(0.1)\\\\& =-20.6\:\: \sf ft/s\end{aligned}`

Question (ii)

Given interval: [2, 2.01]

`\implies t_1=2`

`\implies t_2=2.01`

`\implies s(t_1)=45(2)-16(2)^2=26`

`\implies s(t_2)=45(2.01)-16(2.01)^2=25.8084`

Substitute the values into the formula and solve for v:

`\begin{aligned}\overline{v} & =(s(t_2)-s(t_1))/(t_2-t_1)\\\\\implies \overline{v} & =(s(2.01)-s(2))/(2.01-2)\\\\& =(25.8084-26)/(2.01-2)\\\\& =(-0.1916)/(0.01)\\\\& =-19.16\:\: \sf ft/s\end{aligned}`

Question (iii)

Given interval: [2, 2.001]

`\implies t_1=2`

`\implies t_2=2.001`

`\implies s(t_1)=45(2)-16(2)^2=26`

`\implies s(t_2)=45(2.001)-16(2.001)^2=25.980984`

Substitute the values into the formula and solve for v:

`\begin{aligned}\overline{v} & =(s(t_2)-s(t_1))/(t_2-t_1)\\\\\implies \overline{v} & =(s(2.001)-s(2))/(2.001-2)\\\\& =(25.980984-26)/(2.001-2)\\\\& =(-0.019016)/(0.001)\\\\& =-19.016\:\: \sf ft/s\end{aligned}`

Part (b)

`\boxed{\begin{minipage}{5cm}\underline{Instantaneous velocity formula}\\\\$v_i=\lim_(\triangle t \to 0) \frac{\text{d}s}{\text{d}t}$\end{minipage}}`

To find the equation for instantaneous velocity, differentiate the function for height:

`\begin{aligned}s(t) & =45t-16t^2\\\implies \frac{\text{d}s}{\text{d}t} & = 1 \cdot 45t^(1-1) - 2 \cdot 16t^(2-1)\\v_i& = 45-32t\end{aligned}`

To find the instantaneous velocity when t = 2, substitute t = 2 into the found instantaneous velocity equation:

`\begin{aligned}v_i & =45-32(t)\\t=2\implies v_i & = 45-32(2)\\& = 45-64\\& = -19\:\: \sf ft/s\end{aligned}`

`\boxed{\begin{minipage}{4.8 cm}\underline{Differentiating $ax^n$}\\\\If $y=ax^n$, then $\frac{\text{d}y}{\text{d}x}=nax^(n-1)$\\\end{minipage}}`