Answer:
Part a.
i. -20.6(m/s).
ii. -19.16(m/s).
iii. -19.016(m/s).
Part b.
-19m/s.
Explanation:
Let's refer to the average velocity formula:
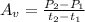 ; where
; where
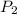 and
and
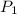 are the final position, and initial position, respectively. Also,
are the final position, and initial position, respectively. Also,
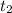 and
and
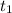 are the final time, and initial time, respectively.
are the final time, and initial time, respectively.
For part (i).
1. Find
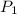 and
and
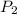 .
.
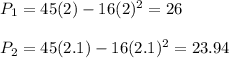
2. Calculate average velocity.
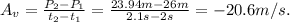
--------------------------------------------------------------------------------------------------
For part (ii).
1. Find
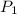 and
and
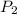 .
.
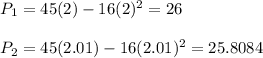
2. Calculate average velocity.
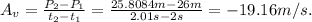
--------------------------------------------------------------------------------------------------
For part (iii).
1. Find
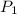 and
and
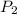 .
.
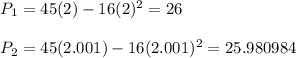
2. Calculate average velocity.
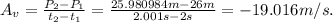
--------------------------------------------------------------------------------------------------
For part b.
Formula of instantaneous velocity:
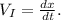
The instantaneous velocity indicates that we need to find the derivative with respect to time (t) of the position equation, and evaluate it for the indicated time. Let's do that:
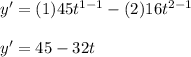
Now, we evaluate for the indicated time (t= 2).
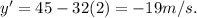
Hence, the instantaneous velocity for t= 2 is -19m/s.