Question

3,6,11,18,27,38

I know the pattern is something like +3, +3+2, 3+4...etc but how do I write that to show the pattern? or do I just put that?​

Answer 1

Answer: The pattern is x^2+2

where x is the term number

Example: the 5th term is 27 because x = 5 leads to x^2+2 = 5^2+2 = 27

=================================================

Step-by-step explanation:

• The jump from 3 to 6 is +3
• The jump from 6 to 11 is +5
• The jump from 11 to 18 is +7
• The jump from 18 to 27 is +9
• The jump from 27 to 38 is +11

The pattern of jumps is: 3, 5, 7, 9, 11

Those increments are going up by 2 each time.

Since we have a consistent pattern of increments, this means that the sequence follows a quadratic model.

Quadratics are stuff like x^2+7x+10 or 3x^2-7. The leading term has an exponent of 2.

-----------

If x is the term number and y is the term itself, then we have these points

(1,3)

(2,6)

(3,11)

(4,18)

(5,27)

(6,38)

The x coordinates increase by 1 each time. The y coordinates are the terms given by your teacher.

Pick exactly 3 of those points. I'll pick the first 3.

Why 3? Because we'll have 3 unknowns to solve for, in which we'll need 3 equations.

• Plug (x,y) = (1,3) into y = ax^2+bx+c, then simplify. You should get the equation a+b+c = 3
• Repeat for (x,y) = (2,6) and you should get 4a+2b+c = 6
• Repeat for (x,y) = (3,11) and you should get 9a+3b+c = 11

-----------

We have this system of equations

`\begin{cases}a+b+c = 3\\ 4a+2b+c = 6\\9a+3b+c = 11\end{cases}`

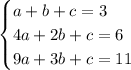
There are a number of methods to solve this system. Substitution is what I'll go for.

Solve the first equation for c

a+b+c = 3

c = 3-a-b

Then use substitution.

4a+2b+c = 6

4a+2b+(3-a-b) = 6

3a+b+3 = 6

3a+b = 6-3

3a+b = 3

and

9a+3b+c = 11

9a+3b+(3-a-b) = 11

8a+2b + 3 = 11

8a+2b = 11-3

8a+2b = 8

We now have this reduced system of equations.

`\begin{cases}3a+b = 3\\8a+2b = 8\end{cases}`

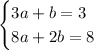
I'll skip the steps as this solution is getting very lengthy as it is. The basic idea is to use substitution again. You should find that a = 1 and b = 0 form the solution set here.

Use those values to find c

c = 3-a-b

c = 3-1-0

c = 2

-----------

To summarize the previous section, we have these solutions:

a = 1, b = 0, c = 2

Therefore the equation y = ax^2+bx+c becomes y = 1x^2+0x+2 aka y = x^2+2. This lets us find any term.

Let's test it out.

• If x = 1, then y = x^2+2 = 1^2+2 = 3
• If x = 2, then y = x^2+2 = 2^2+2 = 6
• If x = 3, then y = x^2+2 = 3^2+2 = 11

And so on. I'll let you test the other x values (4 through 6).

Another way to confirm the answer is to subtract 2 from each item in the original set {3,6,11,18,27,38} and you'll end up with {1,4,9,16,25,36}. This is the list of perfect squares. It shows that term x is simply x^2 but add on 2 so things are adjusted accordingly.

Side note: you can use a tool like GeoGebra or WolframAlpha to quickly solve the system of equations. However, I recommend it only as a means to check your answer rather than do the work for you.