Answer: The pattern is x^2+2
where x is the term number
Example: the 5th term is 27 because x = 5 leads to x^2+2 = 5^2+2 = 27
=================================================
Step-by-step explanation:
- The jump from 3 to 6 is +3
- The jump from 6 to 11 is +5
- The jump from 11 to 18 is +7
- The jump from 18 to 27 is +9
- The jump from 27 to 38 is +11
The pattern of jumps is: 3, 5, 7, 9, 11
Those increments are going up by 2 each time.
Since we have a consistent pattern of increments, this means that the sequence follows a quadratic model.
Quadratics are stuff like x^2+7x+10 or 3x^2-7. The leading term has an exponent of 2.
-----------
If x is the term number and y is the term itself, then we have these points
(1,3)
(2,6)
(3,11)
(4,18)
(5,27)
(6,38)
The x coordinates increase by 1 each time. The y coordinates are the terms given by your teacher.
Pick exactly 3 of those points. I'll pick the first 3.
Why 3? Because we'll have 3 unknowns to solve for, in which we'll need 3 equations.
- Plug (x,y) = (1,3) into y = ax^2+bx+c, then simplify. You should get the equation a+b+c = 3
- Repeat for (x,y) = (2,6) and you should get 4a+2b+c = 6
- Repeat for (x,y) = (3,11) and you should get 9a+3b+c = 11
-----------
We have this system of equations
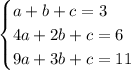
There are a number of methods to solve this system. Substitution is what I'll go for.
Solve the first equation for c
a+b+c = 3
c = 3-a-b
Then use substitution.
4a+2b+c = 6
4a+2b+(3-a-b) = 6
3a+b+3 = 6
3a+b = 6-3
3a+b = 3
and
9a+3b+c = 11
9a+3b+(3-a-b) = 11
8a+2b + 3 = 11
8a+2b = 11-3
8a+2b = 8
We now have this reduced system of equations.
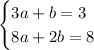
I'll skip the steps as this solution is getting very lengthy as it is. The basic idea is to use substitution again. You should find that a = 1 and b = 0 form the solution set here.
Use those values to find c
c = 3-a-b
c = 3-1-0
c = 2
-----------
To summarize the previous section, we have these solutions:
a = 1, b = 0, c = 2
Therefore the equation y = ax^2+bx+c becomes y = 1x^2+0x+2 aka y = x^2+2. This lets us find any term.
Let's test it out.
- If x = 1, then y = x^2+2 = 1^2+2 = 3
- If x = 2, then y = x^2+2 = 2^2+2 = 6
- If x = 3, then y = x^2+2 = 3^2+2 = 11
And so on. I'll let you test the other x values (4 through 6).
Another way to confirm the answer is to subtract 2 from each item in the original set {3,6,11,18,27,38} and you'll end up with {1,4,9,16,25,36}. This is the list of perfect squares. It shows that term x is simply x^2 but add on 2 so things are adjusted accordingly.
Side note: you can use a tool like GeoGebra or WolframAlpha to quickly solve the system of equations. However, I recommend it only as a means to check your answer rather than do the work for you.