Answer:
1. 3(x+4)=3x+11: No solutions.
2. -2(x+3)=-2x-6: Infinite solutions, any number can make the statement true.
3. 4(x-1) = 1/2(x-8): x= 0.
4. 3x-7=4+6 +4x: x= -17.
Explanation:
Equation 1.
1. Write the expression.
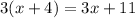
2. Simplify the left side of the equation by applying the associative property of multiplication.
This is the rule we're applying:
 .
.

3. Substract 3x from both sides.
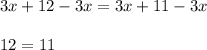
4. Conclude.
As you may notice, we just obtained a false statement in subtitle 3, because 12 doesn't equal 11. Hence, this equation doesn't have solutions.
-------------------------------------------------------------------------------------------------------
Equation 2.
1. Write the expression.
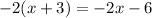
2. Simplify the left side of the equation by applying the associative property of multiplication.
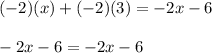
3. Conclude.
Whenever we get an equation that has the same arguments on both sides, this means that there are infinite solutions to this equation, any value of x will make the equation true. Hence, the equation has infinite solutions.
-------------------------------------------------------------------------------------------------------
Equation 3.
1. Write the expression.

2. Simplify the both sides of the equation by applying the associative property of multiplication.

3. Add 4 to both sides.
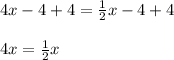
4. Substract
 from both sides.
from both sides.
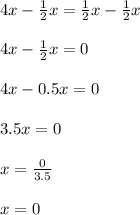
5. Concluide.
The solution for this equation is x= 0.
-------------------------------------------------------------------------------------------------------
Equation 4.
1. Write the expression.
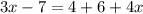
2. Simplify by completing the addition.

3. Add 7 to both sides.
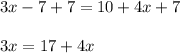
4. Substract 4x from both sides.
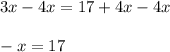
5. Multiply bith sides by -1.
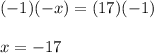
6. Conclude.
The solution of this equation is x= -17.