Question

the common difference in an arithmetic sequence is 8. if the sum of the first 10 terms is 56, find the first term of the sequence

Answer 1

the first term

a₁ = -30.4

Explanation:

Let (an) be an arithmetic sequence with a common difference 8.

a₁ represents its first term.

And let S be the sum of the first 10 terms of the sequence.

Then

S = a₁ + a₂ + ………+ a₁₀

a₁₀ = a₁ + 8(10 - 1) = a₁ + 8×9 = a₁ + 72

S = a₁ + a₂ + ………+ a₁₀

`=(10)/(2) * \left( a_(1)+a_(10)\right)`

`=5} * \left( a_(1)+(a_(1)+72)\right)`

`=5} * \left( 2a_(1)+72\right)`

`=10a_(1)+360`

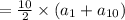
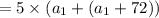
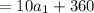
We are given : S = 56

then

56 = 10a₁ + 360

then

-10a₁ = 360 - 56

then

-10a₁ = 304

then

a₁ = -304/10

= -30.4