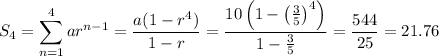Let
 be the first term in the sequence, and
be the first term in the sequence, and
 the common ratio between consecutive terms. Let
the common ratio between consecutive terms. Let
 denote the
denote the
 -th term in the sequence. The first several terms are
-th term in the sequence. The first several terms are
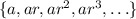
and so the
 -th term is given by
-th term is given by
 .
.
Let
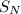 denote the
denote the
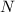 -th partial sum of the series,
-th partial sum of the series,
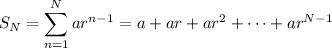
Multiply both sides by
 .
.
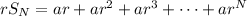
Subtract this from, then solve for,
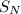 .
.

We know the infinite series converges, so
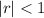 , which means the
, which means the
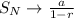 as
as
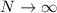 . And since we know the infinite sum is 25, we have
. And since we know the infinite sum is 25, we have
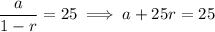
Meanwhile, the sum of the first 2 terms is
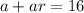
Solve for
 .
.
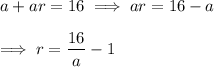
Substitute this into the other equation and solve for
 , then again for
, then again for
 .
.
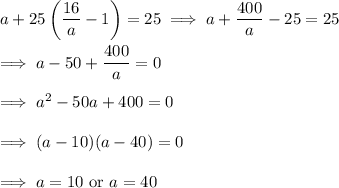
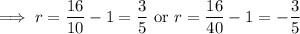
We're given that the ration is positive, so
 and
and
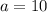 .
.
i) The fifth term in the sequence is
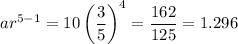
ii) The sum of the first 4 terms is