Question

Between what two consecutive integers must log2(17) lie

Answer 1

4 and 5

Explanation:

For answering questions like this, it can be useful to remember a few of the powers of small integers:

2^4 = 16

2^5 = 32

Exponents and logarithms

A logarithm can be considered to be an exponent of the base.

`\log_b(x) = a \ \Longleftrightarrow\ b^a=x`

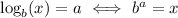
The ordering of powers of 2 relative to the number of interest (17) is ...

16 < 17 < 32

2⁴ < 17 < 2⁵ . . . . . . . . . . . . . . . . . . . expressed as powers of 2

log₂(2⁴) < log₂(17) < log₂(2⁵) . . . . . log₂ of the above inequality

4 < log₂(17) < 5 . . . . . . . . . . . . . . . . showing the values of the logs

Log₂(17) lies between 4 and 5.

__

Additional comment

Using the "change of base" formula, you can use a calculator to find the value of log₂(17). It shows you the value is between 4 and 5.

log₂(17) = log(17)/log(2) . . . . . . using logs to the same base