Question

Write an equation for a line containing (-8, 12) that is perpendicular to the line containing the points (3, 2) and (-7, 2).

Answer 1

x + 8 = 0

Explanation:

Solution:

For Slope of st.line with points (3,2) and (-7,2)

Slope(m1) =

=
`(y_(2)-y_(1))/(x_(2)-x_(1))`

=
`(2-2)/(-7-3)`

= 0

Let slope of the required line by m2

Since the lines are perpendicular to each other

m1*m2= -1

0 * m2 = -1

m2 = -1/0

Now,

Passing point = ( -8,12 )

Using single point form, we get:

`y-y_(1) = m_(2)(x-x_(1))\\or, y-12=(-1)/(0)(x +8)\\ or, Cross multiplying\\or, 0=-x-8\\or, x+8=0`

which is the required equation.

If my answer is wrong You can say it I will try to figure it down

Answer 2

x = - 8

Explanation:

calculate the slope of the line containing the 2 points using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

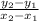
with (x₁, y₁ ) = (3, 2 ) and (x₂, y₂ ) = (- 7, 2 )

m =
`(2-2)/(-7-3)` =
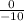`(0)/(-10)` = 0

a line with a slope of zero is a horizontal line parallel to the x- axis

then a perpendicular line will be a vertical line with equation

x = c ( c is the value of the x- coordinates the line passes through )

the line passes through (- 8, 12 ) with x- coordinate - 8 , then

x = - 8 ← equation of perpendicular line