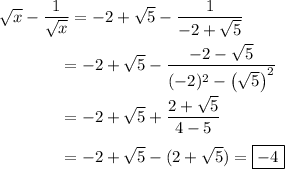Observe that
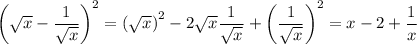
Now,

so that
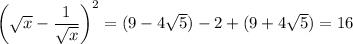
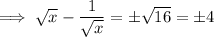
To decide which is the correct value, we need to examine the sign of
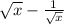 . It evaluates to 0 if
. It evaluates to 0 if
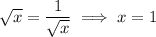
We have
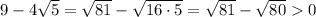
Also,
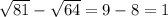
and
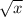 increases as
increases as
 increases, which means
increases, which means
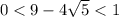
Therefore for all
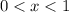 ,
,

For example, when
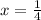 , we get
, we get
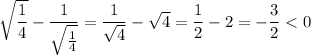
Then the target expression has a negative sign at the given value of
 :
:
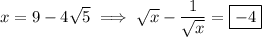
Alternatively, we can try simplifying
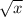 by denesting the radical. Let
by denesting the radical. Let
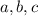 be non-zero integers (
be non-zero integers (
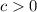 ) such that
) such that
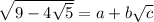
Note that the left side must be positive.
Taking squares on both sides gives
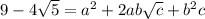
Let
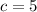 and
and
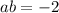 . Then
. Then
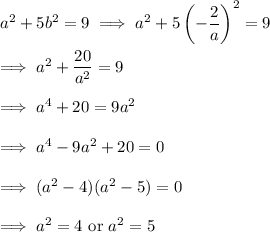
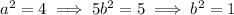
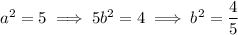
Only the first case leads to integer coefficients. Since
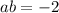 , one of
, one of
 or
or
 must be negative. We have
must be negative. We have
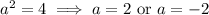
Now if
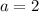 , then
, then
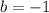 , and
, and
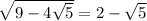
However,
 , so
, so
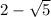 is negative, so we don't want this.
is negative, so we don't want this.
Instead, if
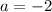 , then
, then
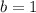 , and thus
, and thus
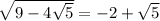
Then our target expression evaluates to