Answer:
110°
Explanation:
The question tells us the angle A and angle B are supplementary angles. This means that the sum of the two angles is 180°.
Set up an Equation and Solve for X
Using this information, we can set up an equation.
Angle A + Angle B = 180
 Combine like Terms
Combine like Terms
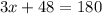 Subtract both sides by 48
Subtract both sides by 48
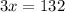 Divide both sides by 3
Divide both sides by 3

Find the Measure of Angle B
We can substitute 61 for x into the given equation for Angle B.
Angle B = 2x + 22
Angle B = 2(44) + 22
Angle B = 88 + 22
Angle B = 110
Check your Work
Angle A + Angle B = 180
44 + 26 + 2(44) + 22 = 180
70 + 88 + 22 = 180
158 + 22 = 180
180 = 180
Therefore ∠B = 110°.