Question

Find the mean, range, and interquartile range of the heights of plants given

below:
2, 22, 4, 36, 82, 44, 65, 30, 8, and 16

Answer 1

Mean: 30.9

Range: 80

Interquartile range: 26

Explanation:

To find the mean, you would add up all the numbers (2, 22, 4, 36, 82, 44, 65, 30, 8, and 16), and divide them by how many numbers are in the collection, which is 10. So you would divide 309 by ten.

To find the range, you find the largest number, which is 82 and subtracts it by the lowest number, 2. That equals 80.

Here is an example of how to find the interquartile range. I hope it helps:

Lower half Median = 71 Upper half

62, 63, 64, 64, 70, 71, 72, 76, 77, 81, 81

Lower quarter Upper quarter

Interquartile range: 77-64=13

Q1 = 64 Q3=77

All credit goes to qbattiste.

Answer 2

Mean = 30.9

Range = 80

Interquartile Range = 36

Explanation:

The mean of a set of numbers is the sum divided by the number of terms. In other words that means 2, 22, 4, 36, 82, 44, 65, 30, 8, 16 go over a fraction like this. There are 10 numbers here so this is our denominator.

`(2+ 22 + 4 + 36 + 82 + 44 + 65 + 30 + 8 + 16)/(10)`

`(309)/(10) > 30.9`

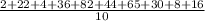
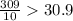
For the range, all we do is subtract the minimum value from the maximum which is 82 - 2. That gives us 80.

For the IQ Range....

Arrange the terms in ascending order.

2, 4, 8, 16, 22, 30, 36, 44, 65, 82

Then we need to find the median which is the average of the two middle terms.

`(22+30)/(2) > (2*11 + 30)/(2) >(2*11+2*15)/(2) > (2 * (11 + 15))/(2) > 11 + 15 > 26`

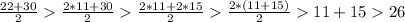
So for the lower half of data 2, 4, 8, 16, 22 we have the median of 8

And for the upper half 30, 36, 44, 65, 82 we have the median of 44.

To find the IQ Range it is the difference between the first quartile (8) and the third (44)

So 44 - 8 = 36