1. According to the plots, the curves intersect when
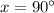 and
and
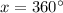 .
.
We can confirm this algebraically.
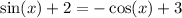
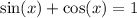
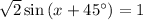


(where
 is an integer)
is an integer)
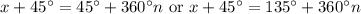
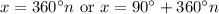
We get the two solutions we found in the interval [0°, 360°] with
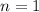 in the first case, and
in the first case, and
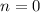 in the second case.
in the second case.
2. We have
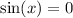 when
when
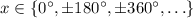 . For the given plot domain [0°, 360°], this happens when
. For the given plot domain [0°, 360°], this happens when
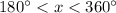 .
.
3. The domain for both equations is all real numbers in general, but considering the given plot, you could argue the domains would be [0°, 360°].
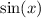 is bounded between -1 and 1, so
is bounded between -1 and 1, so
 is bounded between -1 + 2 = 1 and 1 + 2 = 3, and its range is [1, 3].
is bounded between -1 + 2 = 1 and 1 + 2 = 3, and its range is [1, 3].
Likewise,
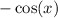 is bounded between -1 and 1, so that
is bounded between -1 and 1, so that
 is bounded between -1 + 3 = 2 and 1 + 3 = 4, so its range would be [2, 4].
is bounded between -1 + 3 = 2 and 1 + 3 = 4, so its range would be [2, 4].