Question

Maths trig functions
please help

Answer 1

1. According to the plots, the curves intersect when
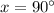`x=90^\circ` and
`x=360^\circ`.

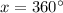We can confirm this algebraically.

`\sin(x) + 2 = -\cos(x) + 3`

`\sin(x) + \cos(x) = 1`

`\sqrt2 \sin\left(x + 45^\circ\right) = 1`

`\sin\left(x + 45^\circ\right) = \frac1{\sqrt2}`

`x + 45^\circ = \sin^(-1)\left(\frac1{\sqrt2}\right) + 360^\circ n \text{ or } x + 45^\circ = 180^\circ - \sin^(-1)\left(\frac1{\sqrt2}\right) + 360^\circ n`

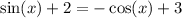
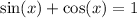
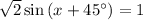
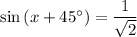
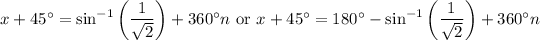
(where
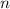`n` is an integer)

`x + 45^\circ = 45^\circ + 360^\circ n \text{ or } x + 45^\circ = 135^\circ + 360^\circ n`

`x = 360^\circ n \text{ or } x = 90^\circ + 360^\circ n`

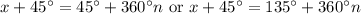
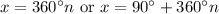
We get the two solutions we found in the interval [0°, 360°] with
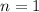`n=1` in the first case, and
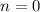`n=0` in the second case.

2. We have
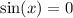`\sin(x)=0` when
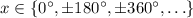`x \in \{0^\circ, \pm 180^\circ, \pm360^\circ, \ldots\}`. For the given plot domain [0°, 360°], this happens when
`180^\circ < x < 360^\circ`.

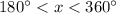3. The domain for both equations is all real numbers in general, but considering the given plot, you could argue the domains would be [0°, 360°].

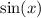`\sin(x)` is bounded between -1 and 1, so
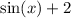`\sin(x) + 2` is bounded between -1 + 2 = 1 and 1 + 2 = 3, and its range is [1, 3].

Likewise,
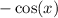`-\cos(x)` is bounded between -1 and 1, so that
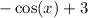`-\cos(x)+3` is bounded between -1 + 3 = 2 and 1 + 3 = 4, so its range would be [2, 4].