Answer:
See attachment for graph.
Explanation:
Given polynomial function:
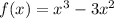
Axis intercepts
The zeros of a function are the points at which the curve crosses the x-axis. To find the zeros, factor the function and set it to zero:
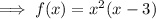
Therefore:
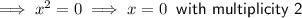
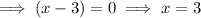
Therefore, the curve intersects the x-axis at x = 3 and has a turning point at (0, 0) since a zero with even multiplicity touches the x-axis and bounces off of the axis.
Note: Since the curve touches the x-axis at (0, 0), the y-intercept is also (0, 0).
End behavior
The end behavior of a function is the behavior the graph of f(x) as x approaches -∞ or +∞.
The degree and the leading coefficient of a polynomial function determine the end behavior of the graph.
As the degree of the given function is odd and the leading coefficient is positive, the end behaviors are:
Turning points
We have already determined that there is a turning point at (0, 0).
To find the other turning point, differentiate the function:
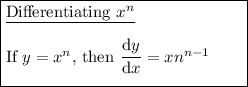

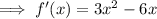
Set the differentiated function to zero and solve for x:

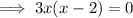
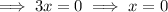
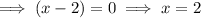
Therefore, there are turning points at x = 0 and x = 2.
Substitute x = 2 into the function to find the y-value of this turning point.

Therefore, the turning points are at (0, 0) and (2, -4).
In Summary
- End behaviors:
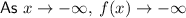
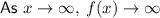
- Turning points at (0, 0) and (2, -4).
- Crosses the x-axis at (3, 0).