Answer:
32 33-cent stamps, 8 23-cent stamps
Explanation:
In order to solve this question, we need to set up a system of equations. Also known as solving for two variables (the number of each stamp).
Let's set x to be the number of 33-cent stamps. Similarly, let's set y to be the number of 23-cent stamps.
To make our first equation, let's think about the number of stamps total we have. We can say:
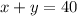
(AKA - The number of 33-cent stamps, plus the number of 23-cent stamps, equals 40 stamps.)
Now, let's make an equation for the cost of these stamps.
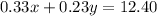
(AKA - The cost of the stamps in total, should equal $12.40).
So now, we have our two equations:
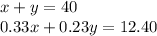
If you have a TI-84 graphing calculator, you can go to apps -> polysmlt2 -> simultaneous eqn solver, and then input these equations into the menu. This will solve the problem for you.
If you need to do this manually, let's use substitution. Condense our first equation to make it more substitutable.
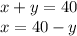
Now, let's put this into our second equation.
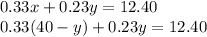
Distribute, and solve for y.
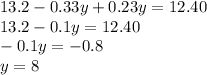
Now, we plug this into one of our equations.
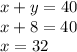
In the end, we have thirty-two 33-cent stamps, and eight 23-cent stamps.