hmmm let;s take a peek at the 1st equation's denominators, hmmm 2 and 4, let's get the LCD for that, that'll be 4.
Now, let's multiply both sides on the 1st equation by the LCD of the denominators, namely 4, to do away with the denominators
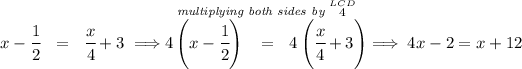
low and behold!!!! the 1st equation is really the 2nd one in disguise.