Question

Determine whether f has an inverse function. If it does, find the inverse function and state any restrictions on its domain.

Answer 1

as you already know, to get the inverse of any expression we start off by doing a quick switcheroo on the variables and then solving for "y", let's do so.

`f(x)=\cfrac{x-7}{x+4}\qquad \implies \qquad y=\cfrac{x-7}{x+4}\qquad \implies \qquad \stackrel{\textit{quick switcheroo}}{x=\cfrac{y-7}{y+4}} \\\\\\ xy+4x=y-7\implies 4x=y-7-xy\implies 4x+7=y-xy \\\\\\ 4x+7=y(1-x)\implies \hspace{5em}\cfrac{4x+7}{1-x}~~ = ~~\stackrel{f^(-1)(x)}{y} ~~ ; ~~ x\\e1`

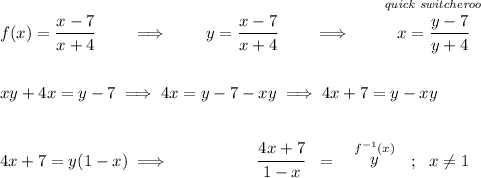
why x ≠ 1? well, if that ever happens our denominator goes to 0 and the fraction goes poof, can't have that.