Question

Find the surface area of a regular hexagon-based pyramid with slant height of 15 cm.

Answer 1

290
`cm^(2)`

Answer:

Solution Given:

The base length [b]=5cm.

The slant height [s]=15cm.

Apothem length [a]=
`(b)/(2Tan((180)/(n)))`

=
`(5)/(2Tan((180)/(6)))`=4.33 cm

Now

the surface area of a regular hexagon-based pyramid=

=3b (a + s)

=3*5(4.33+15)

=289.95≈290
`cm^(2)`

Explanation:

Answer 2

290 cm²

Explanation:

Area of regular hexagon-based pyramid.

First find the area of 6 triangles and then the area of the regular hexagon.

Slant height = s = 15 cm

side = b = 5 cm

`\sf Area \ of \ triangle = (1)/(2)*b* s\\\\Area \ of \ 6 \ triangle = 6*(1)/(2)*b*s\\\\`

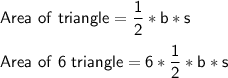
= 3 bs

= 3 * 5 * 15

= 225 cm²

`\sf Area \ of \ regular \ hexagon = (3√(3)b^2)/(2)\\\\`

`\sf =(3*1.732*5*5)/(2)\\\\= 64.95 \ cm^2`

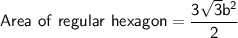
Area of regular hexagon based polygon = Area of 6 triangles + area of regular hexagon

= 225 + 64.95

= 289.95

= 290.0 cm²