Question

The multiplication of three consecutive positive integers equals five times the sum of these numbers. Find the sum of the smallest and the biggest number.

a. 6 b. 7 c.8. d. 9. e.10​

Answer 1

Answer: c. 8.

Explanation:

`Let\ the\ smallest \ number\ be\ x\in\mathbb N.\\Hence,\\x*(x+1)*(x+2)=5*(x+(x+1)+(x+2))\\x*(x+1)*(x+2)=5*(x+x+1+x+2)\\x*(x+1)*(x+2)=5*(3x+3)\\x*(x+1)*(x+2)=5*3*(x+1)\\x*(x+1)*(x+2)=15*(x+1)\\Divide\ both\ parts\ of\ the\ equation\ by\ (x-1)\ ((x-1)\in\mathbb N):`

`x*(x+2)=15\\x^2+2x=15\\x^2+2x-15=0\\x^2+2x+3x-3x-15=0\\x^2+5x-3x-15=0\\x*(x+5)-3*(x+5)=0\\(x+5)*(x-3)=0\\x+5=0\\x_1=-5\\otin\ (x\in\mathbb N)\\x-3=0\\x_2=3\in\mathbb N.\\Hence,\\3,\ (3+1),\ (3+2)\ \Leftrightarrow\ 3,\ 4,\ 5.\\3+5=8.`

Answer 2

c. 8

Explanation:

let x be the smallest positive integer among the three.

Then

Our three numbers are : x , x + 1 , x + 2

The statement “The multiplication of the three consecutive positive integers equals five times the sum of these numbers”

means

x(x + 1)(x + 2) = 5(x + x+1 + x+2)

⇔ x(x + 1)(x + 2) = 5(3x + 3)

⇔ x(x + 1)(x + 2) = 5×3(x + 1)

⇔ (x + 1)(x + 2)x = 15(x + 1)

⇔ (x + 1)(x² + 2x) = 15(x + 1)

⇔ (x + 1)×[x² + 2x - 15] = 0

⇔ x + 1 = 0 or x² + 2x - 15 = 0 (zero product property used)

Solving x + 1 = 0 :

x + 1 = 0 ⇔ x = -1 (reject because x is positive).

Solving x² + 2x - 15 = 0 (Using quadratic formula) :

Discriminant Δ = 2² - 4(1)(-15) = 64 ⇒ √Δ = 8

Then

`x = (-2+8)/(2) \ \ \text{or} \ \ x = (-2-8)/(2)`

Then

`x = 3 \ \ \text{or} \ \ x = -5`

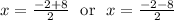
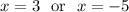
Then

x = 3 (-5 to be rejected because negative)

Conclusion :

The smallest number = x = 3.

The biggest number = x + 2 = 5.

Their sum = 3 + 5 = 8.