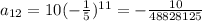Answer:
4.
5th term = -(2/25 x -5) = 2/125
6th term = -2/(125 x - 5) = -2/625
7th term = 2/(625 x-5) = 2/3125
5.
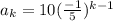
6 .
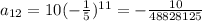
Explanation:
This is a geometric sequence with the common ratio 1/5 and sign that changes every alternate term. We can also state that the common ratio is -
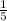
First term is 10 with +ve sign
Second term is 10/5 with negative sign = -2
Third term is -2/5 with positive sign = 2/5
Fourth term is 2/5 ÷ 5 = 2/25 with negative sign = -2/25
4. Since each subsequent term = (-1/5) x (previous term) we have
5th term = -(2/25 x -5) = 2/125
6th term = -2/(125 x - 5) = -2/625
7th term = 2/(625 x-5) = 2/3125
5. General equation
Let
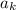 be the kth term
be the kth term
Since this is a geometric sequence, the general equation is

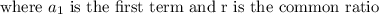
so the equation is
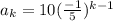
6. The 12 term is calculated as