Question

Is 0.9707320412481934... is rational or irrational and give a
reason why

Answer 1

irrational, it is unrepeating and also unended

Answer 2

irrational

Explanation:

A rational number is one that can be expressed exactly using a finite number of digits, without any symbols such as π or √ or ∛.

Repeating decimals

When a rational number is expressed as a decimal, it will have a repeating decimal fraction if its denominator is something other than a product of powers of 2 and 5. For example, 3/19 as a decimal is ...

0.157894736842105263 157894736842105263 ...(18-digit repeat)

The length of the sequence of repeating digits can be quite long, sometimes as long as 1 less than the fraction's denominator. (The fraction below might have more than 83 million digits in its repeating decimal.) Many calculators and spreadsheets cannot show more than about 16 digits, so long repeating decimal fractions may look like they don't repeat at all.

The given decimal fraction could be the first part of a very long repeating decimal. The digits shown are the first 16 digits of the decimal representation of ...

`(80941747)/(83382173) \approx 0.9707320412481934\,237909582903290 \dots \text{ very long repea}\text{t}`

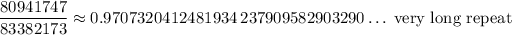
Usually, but not always, such numbers are accompanied by an indication they are repeating decimals, or derived from rational numbers.

Known repeating digits are sometimes represented using an overbar:

`(1)/(7)=0.\overline{142857}\qquad\text{a 6-digit repea}\text{t}`

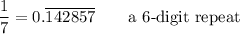
Non-repeating decimals

A decimal fraction of indeterminate length is usually indicated by "..." at the end of a string of its digits. That is the case here. It usually signifies there are an infinite number of digits, with no known repeating pattern. When the number of digits is infinite, and it is known there is not a repeating pattern, then it can be concluded that the number is irrational.

__

Additional comment

In short, without knowing the intended meaning of the "...", and without knowing where the number came from, we cannot be sure of the rational/irrational status of the number. Very long repeating decimal fractions can arise in the normal course of rational number arithmetic. Many solutions to polynomial, trig, or exponential equations are irrational numbers.

Either of these kinds of numbers may be reported using "..." to indicate there's more to the number than the digits shown.