Question

if a Firebird travels at a velocity of 0 to 60 mph in four seconds traveling east what was the acceleration of the Firebird

Answer 1

6.7 m/s^2

Step-by-step explanation:

The formula of acceleration is:

`\displaystyle{\vec{a} = \frac{\Delta \vec{v}}{\Delta t} = (v_2 - v_1)/(t_2-t_1)}`

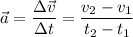
where
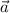`\displaystyle{\vec{a}}` is acceleration,
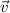`\displaystyle{\vec{v}}` is velocity and
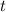`\displaystyle{t}` is time.
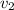`\displaystyle{v_2}` means final velocity.
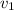`\displaystyle{v_1}` means initial velocity,
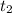`\displaystyle{t_2}` means final time and
`\displaystyle{t_1}` means initial time.

We are given that the Firebird travels at velocity of 0 to 60 mph in four seconds. Therefore:

• Our initial velocity starts at 0 mph.
• Our final velocity is at 60 mph.
• Our initial time is 0 second.
• Our final time is 4 seconds.

Since it travels to the east then our vector will be positive. However, acceleration has to be in m/s^2 unit (Sl unit) so we'll have to convert from mph (miles per hours) to m/s (meters per second) first.

We know that:

• A mile equals to 1609.344 meters.
• An hour equals to 60 minutes which a minute equals to 60 seconds. So 60 minutes will equal to 3600 seconds.

Now we divide 1609.344 by 3600 to find a unit rate of m/s:

`\displaystyle{(1609.344)/(3600) \ \, \sf{m/s}}\\\\\displaystyle{= 0.44704 \ \, \sf{m/s}}`

Now multiply 0.44704 m/s by 0 and 60 to get velocity in m/s unit:

• Initial velocity = 0 m/s
• Final velocity = 60 * 0.44704 = 26.82 m/s

Time is already in second so no need for conversion. Substitute known information in the formula:

`\displaystyle{\vec{a} = (26.82-0)/(4-0)}\\\\\displaystyle{\vec{a} = (26.82)/(4)}\\\\\displaystyle{\vec{a} = 6.7 \ \, \sf{m/s^2}}`

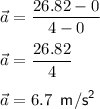
Therefore, the Firebird will accelerate at the rate of 6.7 m/s^2.