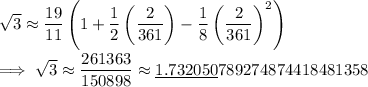We have the binomial series
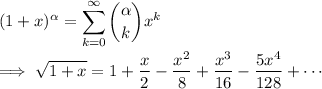
valid for
 , where
, where

We would get √3 on the left by replacing
 , but sadly that's outside the radius of convergence of the series on the right...
, but sadly that's outside the radius of convergence of the series on the right...
However, playing around with √3 we can write
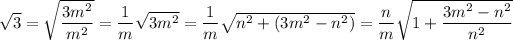
for some positive integers
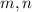 .
.
If we choose reasonable values of
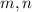 such that
such that
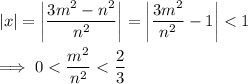
we can then apply the binomial series to get - say, for the first 3 terms -
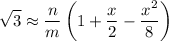
For example, we can try
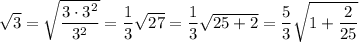
so that
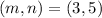 and
and
 . Then the series gives the approximation
. Then the series gives the approximation
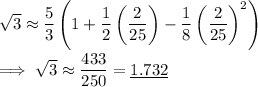
Compare this to the more accurate value of
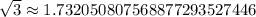
which tells us we're off by an error of less than
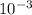 .
.
As another example,
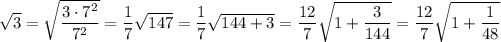
which gives
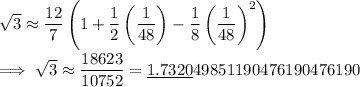
One more example for good measure:

Then