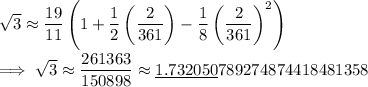Question

Use the binomial expansion and approximation to find √3​

Answer 1

We have the binomial series

`(1 + x)^\alpha = \displaystyle \sum_(k=0)^\infty \binom \alpha k x^k \\\\ \implies √(1+x) = 1 + \frac x2 - \frac{x^2}8 + (x^3)/(16) - (5x^4)/(128) + \cdots`

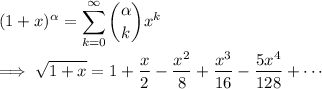
valid for
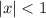`|x|<1`, where

`\dbinom \alpha k = (\alpha (\alpha-1)(\alpha-2)\cdots(\alpha-(k-1)))/(k!)`

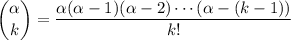
We would get √3 on the left by replacing
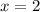`x=2`, but sadly that's outside the radius of convergence of the series on the right...

However, playing around with √3 we can write

`\sqrt3 = \sqrt{(3m^2)/(m^2)} = \frac1m √(3m^2) = \frac1m √(n^2 + (3m^2-n^2)) = \frac nm \sqrt{1 + (3m^2-n^2)/(n^2)}`

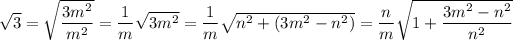
for some positive integers
`m,n`.

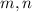If we choose reasonable values of
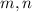`m,n` such that

`|x| = \left|(3m^2 - n^2)/(n^2)\right| = \left|(3m^2)/(n^2) - 1\right| < 1 \\\\ \implies 0 < (m^2)/(n^2) < \frac23`

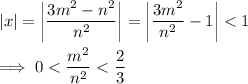
we can then apply the binomial series to get - say, for the first 3 terms -

`\displaystyle \sqrt3 \approx \frac nm \left(1 + \frac x2 - \frac{x^2}8\right)`

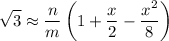
For example, we can try

`\sqrt3 = \sqrt{(3\cdot3^2)/(3^2)} = \frac1{3} √(27) = \frac1{3} √(25 + 2) = (5)/(3) \sqrt{1 + \frac2{25}}`

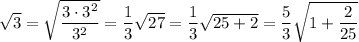
so that
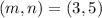`(m,n) = (3,5)` and
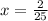`x=\frac2{25}`. Then the series gives the approximation

`\displaystyle \sqrt3 \approx \frac53 \left(1 + \frac12\left(\frac2{25}\right) - \frac18\left(\frac2{25}\right)^2\right) \\\\ \implies \sqrt3 \approx (433)/(250) = \underline{1.732}`

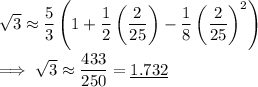
Compare this to the more accurate value of

`\sqrt3 \approx 1.732050807568877293527446`

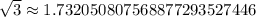
which tells us we're off by an error of less than
`10^(-3)`.

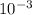As another example,

`\sqrt3 = \sqrt{(3\cdot7^2)/(7^2)} = \frac17 √(147) = \frac17 √(144 + 3) = \frac{12}7 \sqrt{1 + \frac3{144}} = \frac{12}7 \sqrt{1 + \frac1{48}}`

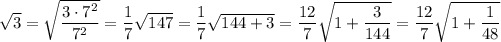
which gives

`\displaystyle \sqrt3 \approx \frac{12}7 \left(1 + \frac12\left(\frac1{48}\right) - \frac18\left(\frac1{48}\right)^2\right) \\\\ \implies \sqrt3 \approx (18623)/(10752) = \underline{1.7320}49851190476190476190`

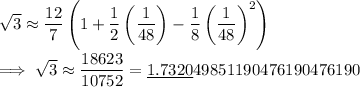
One more example for good measure:

`\sqrt3 = \sqrt{(3\cdot11^2)/(11^2)} = \frac1{11} √(363) = \frac1{11} √(361 + 2) = (19)/(11) \sqrt{1 + \frac2{361}}`

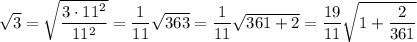
Then

`\displaystyle \sqrt3 \approx (19)/(11) \left(1 + \frac12\left(\frac2{361}\right) - \frac18\left(\frac2{361}\right)^2\right) \\\\ \implies \sqrt3 \approx (261363)/(150898) \approx \underline{1.732050}789274874418481358`