Hi, there!
_______
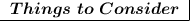
- Does 68 have any perfect squares inside it? If so, what are they?
(1)
68 can be written as:
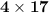
Thus,
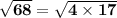
Now, what did we do that for?
We don't know the square root of 17, but the square root of 4 we know!
Thus,
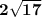
Out of the four options, we choose
◉ D.
Hope the answer - and explanation - made sense to you,
happy studying!!