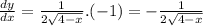Answer:
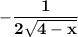
Explanation:
This can also be solved without using limits
Let
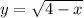
The power rule of derivatives says that if we have a function
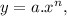
then the first derivative given by
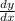 or abbreviated as
or abbreviated as
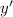 is given by
is given by
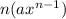
We can use this in combination with the substitution rule of calculus
Let u = 4-x
Then we have
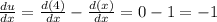
(First differential of a constant is 0 and first differential of x is 1)
Substituting for u in the original expression
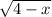 we get
we get
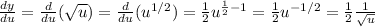
The substitution rule states
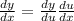
So
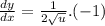
Substituting for u in terms of x we get