Question

Find the first derivative of the function

`f(x) = √(4 - x)`
​

Answer 1

`\bold{-(1)/(2√(4-x))}`

Explanation:

This can also be solved without using limits

Let
`y = √(4-x)`

The power rule of derivatives says that if we have a function

`y = a.x^n,`

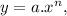
then the first derivative given by
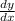`(dy)/(dx)` or abbreviated as
`y'` is given by
`n(ax^(n-1))`

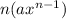
We can use this in combination with the substitution rule of calculus

Let u = 4-x

Then we have
`(du)/(dx) = (d(4))/(dx) - (d(x))/(dx) = 0 -1 = -1`

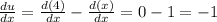
(First differential of a constant is 0 and first differential of x is 1)

Substituting for u in the original expression
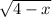`√(4-x)` we get
`(dy)/(du) = (d)/(du) (√(u)) = (d)/(du)(u^(1/2)) = (1)/(2) u^{(1)/(2) -1} = (1)/(2) u^(-1/2) =(1)/(2) (1)/(√(u) )`

The substitution rule states
`(dy)/(dx) = (dy)/(du) (du)/(dx)`

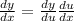
So

`(dy)/(dx) = (1)/(2√(u) ) . (-1)`

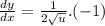
Substituting for u in terms of x we get

`(dy)/(dx) = (1)/(2√(4-x) ) . (-1) = -(1)/(2√(4-x))`

Answer 2

Explanation:

Check the attachment for answer