Answer:
A
Explanation:
Our function is
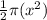
We need to estimate v(2.98) using V(3).
Variables:
What we are trying to find is V(2.98). We will later plug in 2.98 into the tangent line approximation.
We are going to use V'(3) for the slope of the tangent line. We will use V(3) later for the tangent line approximation.
So first, let solve for
V'(x).
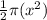
1/2 pi is a constant so
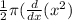

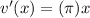
Let x=3,
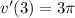
Let find v(3).
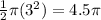
The tangent line equation is
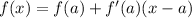
x is 2.8
a. is 3.
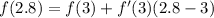
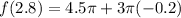
Disclaimer: F(x) is V(x).
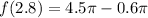
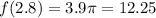
The closest here is A