Answer:
S₁₆ = 328
Explanation:
the nth term of an arithmetic sequence is
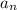 = a₁ + (n - 1)d
= a₁ + (n - 1)d
where a₁ is the first term and d the common difference
given a₄ = 7 and a₇ = 16 , then
a₁ + 3d = 7 → (1)
a₁ + 6d = 16 → (2)
subtract (1) from (2) term by term to eliminate a₁
0 + 3d = 9
3d = 9 ( divide both sides by 3 )
d = 3
substitute d = 3 into (1) and solve for a₁
a₁ + 3(3) = 7
a₁ + 9 = 7 ( subtract 9 from both sides )
a₁ = - 2
the sum to n terms of an arithmetic sequence is
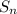 =
=
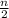 [ 2a₁ + (n - 1)d ]
[ 2a₁ + (n - 1)d ]
with a₁ = - 2 and d = 3 , then
S₁₆ =
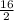 [ (2 × - 2) + (15 × 3) ]
[ (2 × - 2) + (15 × 3) ]
= 8(- 4 + 45)
= 8 × 41
= 328