Can you define f(0, 0) = c for some c that extends f(x, y) to be continuous at (0, 0)? If so, for what value of c? If not, explain why.

Question

asked Jun 24, 2023 81.9k views

1 Answer

Steenhulthin · Answer 1 · 2023-06-28T02:40:34+0000

(i) Yes. Simplify
f(x,y) .

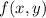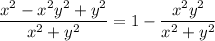
$\displaystyle (x^2 - x^2y^2 + y^2)/(x^2 + y^2) = 1 - (x^2y^2)/(x^2 + y^2)$

Now compute the limit by converting to polar coordinates.

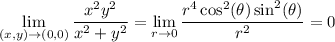
$\displaystyle \lim_((x,y)\to(0,0)) (x^2y^2)/(x^2+y^2) = \lim_(r\to0) (r^4 \cos^2(\theta) \sin^2(\theta))/(r^2) = 0$

This tells us

$\displaystyle \lim_((x,y)\to(0,0)) f(x,y) = 1$

so we can define
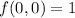f(0,0)=1 to make the function continuous at the origin.

Alternatively, we have

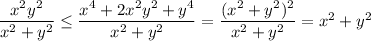
$(x^2y^2)/(x^2+y^2) \le (x^4 + 2x^2y^2 + y^4)/(x^2 + y^2) = ((x^2+y^2)^2)/(x^2+y^2) = x^2 + y^2$

and

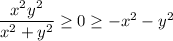
$(x^2y^2)/(x^2+y^2) \ge 0 \ge -x^2 - y^2$

Now,

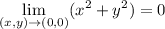
$\displaystyle \lim_((x,y)\to(0,0)) -(x^2+y^2) = 0$

$\displaystyle \lim_((x,y)\to(0,0)) (x^2+y^2) = 0$

so by the squeeze theorem,

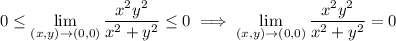
$\displaystyle 0 \le \lim_((x,y)\to(0,0)) (x^2y^2)/(x^2+y^2) \le 0 \implies \lim_((x,y)\to(0,0)) (x^2y^2)/(x^2+y^2) = 0$

and
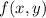f(x,y) approaches 1 as we approach the origin.

(ii) No. Expand the fraction.

$\displaystyle (x^2 + y^3)/(xy) = \frac xy + \frac{y^2}x$

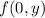f(0,y) and
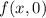f(x,0) are undefined, so there is no way to make
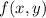f(x,y) continuous at (0, 0).

(iii) No. Similarly,

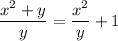
$\frac{x^2 + y}y = \frac{x^2}y + 1$

is undefined when
y=0 .