Question

If (a + b)/(a - b) = (a - b)/(a + b) then, the value of (ab) ^ 4 will be: reply as soon as possible by explaining ​

Answer 1

0

Explanation:

So we have the equation:

`((a+b))/((a-b))=((a-b))/((a+b))`

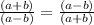
We can cross multiply to get the following equation:

`(a-b)^2=(a+b)^2`

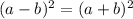
We can take the square root of both sides

`a-b=a+b`

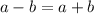
Add b and subtract a to both sides:

`0=2b`

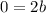
0 = b

If we plug in 0 as b

we get the following equation:

`(a+0)/(a-0)=(a-0)/(a+0)`

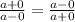
which is just:

`(a)/(a) = (a)/(a)`

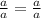
which is valid for all values except:
`a\\e0`

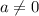
since b=0, then we get the equation:
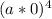`(a * 0)^4` which is just:
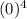`(0)^4` which is just 0

We took the positive solution, to the square root, but what if we had taken the negative solution?

Well we would've gotten the equation:

`-(a-b)=-(a+b)`

Distributing the signs we get:

`-a+b=-a-b`

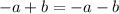
Add a to both sides

`b=-b`

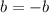
looking at this, it's obvious the only solution is 0, but we can also just add b to both sides

2b = 0

Now divide both sides by 2

b = 0

This gives us the same thing, and we can come to the same reasoning

The last thing to note is that, if a=0, then we have the fractions:

`(0+b)/(0-b)=(0-b)/(0+b) = (b)/(-b)=(-b)/(b)`

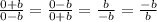
This equations are the exact same, since if we move the sign to the front we just get:
`-(b)/(b)=-(b)/(b)`

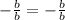
This works for all real numbers except when b=0

Since a=0 in all these cases, we get the equation:

(0 * b) ^ 4 = (0)^4 = 0