Answer:
x=3
Explanation:
Set equations equal to each other:
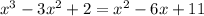
Subtract two from both sides
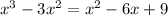
Factor out x^2 from the left side
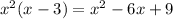
Factor the right side, look for two factors of 9, which add to -6, which is just -3 and-3
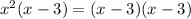
So as you can see here, we have both sides in factored form, and both have a factor of (x-3) on both sides, and if one of the factors is zero, then the entire thing becomes zero, since 0 * anything= zero.
this means a solution would be at x=3, since it makes the right side 0 * 0 = 0, and the left side (3)^2 * 0 = 0
It's important to notice this, since had we divided by x-3 to make the equation a quadratic, we would've excluded this real solution, because when dividing by x-3 the solution x=3 makes it 0, so we would've been dividing by zero.
So one of the real solutions is at x=3