Answer:
525
Explanation:
This is a question involving combinatorics
The number of ways of choosing a subset k from a set of n elements is given by
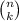 which evaluates to
which evaluates to
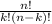
n! is the product n × (n-1) × (n-2) x....x 3 x 2 x 1
For example,
4! = 4 x 3 x 2 x 1 = 24
3! = 3 x 2 x 1 = 6
Since we have to choose 4 boys from a class of 6 boys, the total number of ways this can be done is
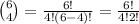
Note that 6! = 6 x 5 x 4 x 3 x 2 x 1 and 4 x 3 x 2 x 1 is nothing but 4!
So the numerator can be re-written as 6 x 5 x (4!)
We can rewrite the expression
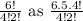
Cancelling 4! from both numerator and denominator gives us the result
as (6 × 5)/2! = 20/2 = 15 different ways of choosing 4 boys from a class of 6 boys
For the girls, the number of ways of choosing 3 girls from a class of 7 girls is given by
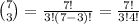
This works out to (7 x 6 x 5 )/(3 x 2 x 1) (using the same logic as for the boys computation)
= 210/6 = 35
So total number of committees of 4 boys and 3 girls that can be formed from a class of 6 boys and 7 girls = 15 x 35 = 525