Question

Please help dont understand!​

Answer 1

`\bold{Answer} \downarrow`

`Length\ of\ Arc\ ADB = \large\boxed{(68\pi)/(9) }`

`Area\ of\ shaded\ region= \large\boxed{(136\pi)/(9) }`

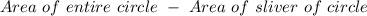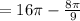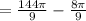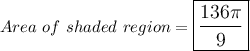
Formulas needed:

`Arc\ length=\boxed{2\pi r((\theta)/(360) )}`

`Area \ of\ a\ sector=\boxed{((n)/(360))*\pi * r^2}`

`Area\ of\ Circle=\boxed {\pi* r^2}`

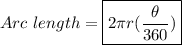
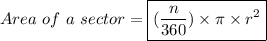
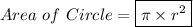
Explanation:

First, let's find the arc length:

`Arc\ length=2\pi r((\theta)/(360))`

`=2\pi (4)((340)/(360))`

`=2\pi (4)((17)/(18))`

`=2\pi((68)/(18))`

`=(136\pi )/(18)`

`\longrightarrow \large\boxed{(68\pi)/(9) }`

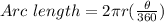
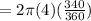
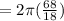
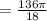
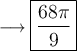
Next, let's find the area of the sliver of the circle we just found the arc length of.

`Area \ of\ a\ sector=((n)/(360))*\pi * r^2`

`=((20)/(360) )* \pi * 4^2`

`=((1)/(18))* \pi * 16`

`=(16\pi)/(18)`

`\longrightarrow (8 \pi)/(9)`

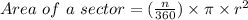
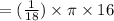
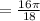
Finally, find the area of the entire circle and subtract the sliver area by that.

`Area\ of\ Circle= {\pi* r^2`

`=\pi * 4^2`

`\longrightarrow16\pi`

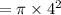
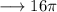
Subtracting the area by the sliver.

`Area\ of\ entire\ circle \ -\ Area\ of\ sliver\ of\ circle`

`=16\pi -(8\pi)/(9)`

`=(144\pi)/(9) -(8\pi )/(9)`

`\longrightarrow \large\boxed{(136\pi)/(9) }`

Answer 2

Explanation:

C = 2 π r

A = π r²

~~~~~~~~~~~

(1). C = 8 π

Let the length of the arc ADB is "x"

x = ( 8π ÷ 360° ) × 340°

x =
`(68)/(9) \pi`

(2). A = 16 π

The area of shaded region is

( 16 π ÷ 360° ) × 340° =
`(136)/(9) \pi`