Check the picture below.
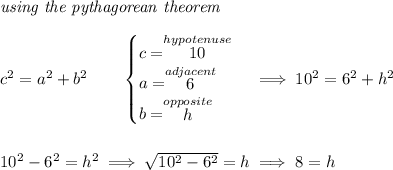
first off let's check what "h" is in the triangular face.
so, the gazebo has 4 squarish faces, each 12x12, recall 48 ÷ 4 = 12, and it has 4 triangular faces, each with a height of 8 and a base of 12.
notice we're skipping the top and bottom of the cube and the bottom of the pyramid because they're not part of the "surface area".
![\stackrel{\textit{\large Areas}}{\stackrel{\textit{4 triangular faces}}{4\left[\cfrac{1}{2}(12)(8) \right]}~~~~+~~~~\stackrel{\textit{4 squarish faces}}{4[12\cdot 12]}}\implies 192+576\implies 768](https://img.qammunity.org/2023/formulas/mathematics/high-school/ld5folu3rwgjhneuo3wty4a23utpx0s4uj.png)