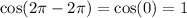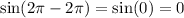The period of
 is
is
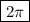 .
.
Recall that
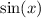 and
and
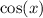 both have periods of
both have periods of
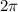 . This means
. This means
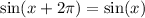
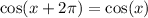
Replacing
 with
with
 , we have
, we have
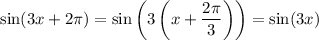
In other words, if we change
 by some multiple of
by some multiple of
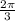 , we end up with the same output. So
, we end up with the same output. So
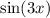 has period
has period
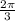 .
.
Similarly,
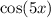 has a period of
has a period of
 ,
,
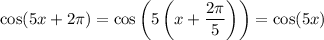
We want to find the period
 of
of
 , such that
, such that

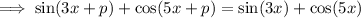
On the left side, we have
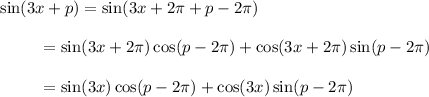
and

So, in terms of its period, we have
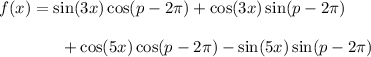
and we need to find the smallest positive
 such that
such that
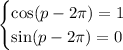
which points to
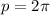 , since
, since