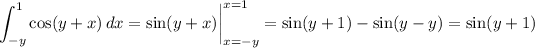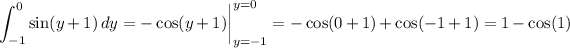One way to capture the domain of integration is with the set
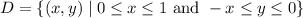
Then we can write the double integral as the iterated integral
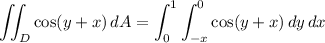
Compute the integral with respect to
 .
.
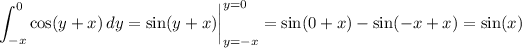
Compute the remaining integral.

We could also swap the order of integration variables by writing
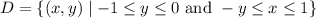
and
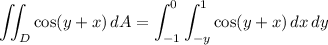
and this would have led to the same result.