I'm not sure if the last two apostrophes are part of the quote - "Solve ... " - or if you mean the second derivative
 . I think you mean the first interpretation, but I'll include both cases since they are both solvable.
. I think you mean the first interpretation, but I'll include both cases since they are both solvable.
If the former is correct, separate variables to solve.

Integrate both sides to get
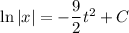
Solve for
 .
.

If you meant the latter, then the ODE can be rewritten as

Reduce the order of the equation by substituting
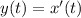 and
and
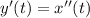 .
.
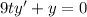
Solve for
 and separate variables.
and separate variables.
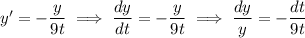
Integrate.
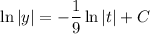
Solve for
 .
.
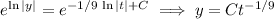
Solve for
 by integrating.
by integrating.
