Is f(x)= \sqrt{5-x^(2) } a one to one function?

Question

Is f(x)=
`\sqrt{5-x^(2) }` a one to one function?

Answer 1

No, it is not a one-to-one function.

Explanation:

A one-to-one function means a value of y will only exist one value of x. This means that a value of y will only have one value of x.

An example of one-to-one function is an odd-degree polynomial such as linear function.

An example of non one-to-one function is a parabola since a value of y exists two values of x.

From the question, this function represents a graph of half circle with radius equal to
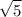`\displaystyle{√(5)}`. (The graph has been attached below for visual reference.)

There's also a way to determine whether if a function is one-to-one or not. This can be done by drawing a horizontal line.

• If a horizontal line and a graph have one common point then it's a one-to-one function
• Otherwise (having more than one common points), a function is not a one-to-one.

From the graph and a horizontal line, both have two common points. Therefore, the function is not a one-to-one function.

* The red graph represents the given function while blue graph is a horizontal line determining a one-to-one function or not *