Answer:
x = 7
Explanation:
since the points all lie on the same line then the slopes of adjacent points will have the same slope.
calculate the slope using R and S then equate to slope using R and T or S and T
calculate slope using slope formula
m =
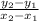
with (x₁, y₁ ) = R (- 5, - 3 ) and (x₂, y₂ ) = S (- 1, - 1 )
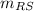 =
=
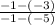 =
=
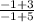 =
=
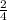 =
=

Repeat with (x₁, y₁ ) = R (- 5, - 3 ) and (x₂, y₂ ) = T (x, 3 )
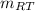 =
=
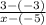 =
=
 =
=

equating
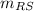 and
and
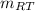
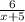 =
=
 ( cross- multiply )
( cross- multiply )
x + 5 = 12 ( subtract 5 from both sides )
x = 7