Question

HELP!!!! Which of the following statements must be true to prove lines m and n are parallel? Question 19 options: A) ∠1 ≅ ∠6 B) m∠3 + m∠5 = 180° C) m∠2 + m∠6 = 180° D) ∠4 ≅ ∠8

Answer 1

Answer: B) m∠3 + m∠5 = 180°

Explanation:

Concept:

For this question, we will be looking at each answer choice and eliminating the incorrect ones

A) ∠1 ≅ ∠6

∠1 is an exterior angle

∠6 is an interior angle

They are in an alternative position

Since they are neither both exterior nor interior, they are not congruent

`\large\boxed{FALSE}`

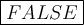
B) m∠3 + m∠5 = 180°

∠3 is an interior angle

∠5 is an interior angle

They are in a same-side position

Since they are both interiors, they fulfill the same-side interior angle theorem, which states: that if a transversal cuts two parallel lines, then the interior angles on the same side of the transversal are supplementary, which means their sum adds up to 180°.

`\Huge\boxed{TRUE}`

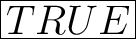
C) m∠2 + m∠6 = 180°

∠2 is an exterior angle

∠6 is an interior angle

They are in a same-side position

Since they are on the same side, they fulfill the corresponding angle theorem which states: the angles that occupy the same relative position at each intersection are congruent to each other.

However, they are only congruent, they don't add up to 180°

`\large\boxed{FALSE}`

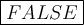
D) ∠4 ≅ ∠8

∠4 is an interior angle

∠8 is an exterior angle

They are in an alternative position

Since they are neither both exterior nor interior, they are not congruent

`\large\boxed{FALSE}`

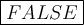
Hope this helps!! :)

Please let me know if you have any questions