Observe that the given vector field is a gradient field:
Let
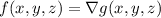 , so that
, so that
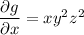
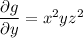
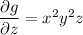
Integrating the first equation with respect to
 , we get
, we get
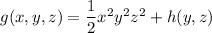
Differentiating this with respect to
 gives
gives

Now differentiating
 with respect to
with respect to
 gives
gives
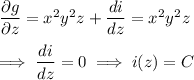
Putting everything together, we find a scalar potential function whose gradient is
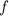 ,
,
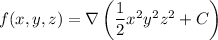
It follows that the curl of
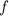 is 0 (i.e. the zero vector).
is 0 (i.e. the zero vector).