Answer: A = 33 in²
Explanation:
Given information:
Longer side = 7 in
Shorter side = 4 in
Shorter Hypotenuse = 5 in
Given formula:
A = (1/2) × (d₁) × (d₂)
- A = area
- d₁ = The longer line (horizontal)
- d₂ = The shorter line (vertical)
Please refer to the attachment below for a graphical understanding
Determine the length of the shorter side (vertical) through the Pythagorean theorem
a² + b² = c² (Pythagorean theorem)
(4)² + b² = (5)² (Substitute values into the equation)
16 + b² = 25
b² = 25 - 16
b² = 9
b = 3 or b = -3 (rej)
Substitute values into the given formula
A = (1/2) × d₁ × d₂
A = (1/2) × (7 + 4) × (3 + 3)
Simplify values in the parenthesis
A = (1/2) × 11 × 6
Simplify by multiplication
A = (11/2) × 6
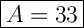
Hope this helps!! :)
Please let me know if you have any questions